【题目】

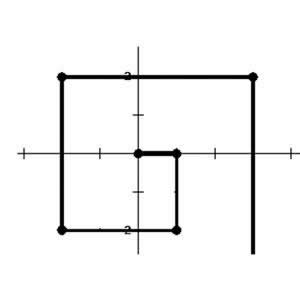
一个人站在坐标（0, 0）处，面朝 x 轴正方向。第一轮，他向前走 1 单位距离，然后右转；第二轮，他向前走 2 单位距离，然后右转；第三轮，他向前走 3 单位距离，然后右转……他一直这么走下去。请问第 2017 轮后，他的坐标是：（ ）。

【解析】

坐标系概念：

相交于原点的两条数轴，构成了平面放射坐标系。如两条数轴上的度量单位相等，则称此放射坐标系为笛卡尔坐标系。
两条数轴互相垂直的笛卡尔坐标系，称为笛卡尔直角坐标系。
两个坐标轴的相交点，称为原点，通常标记为 O ，是英语“Origin”的首字母。

1. 列出走法的每一步：

第1步：X轴坐标值 + 1
第2步：Y轴坐标值 – 2
第3步：X轴坐标值 – 3
第4步：Y轴坐标值 + 4
第5步：X轴坐标值 + 5 ， Y轴坐标值与上一步第4步相同
第6步：Y轴坐标值 – 6
第7步：X轴坐标值 – 7
第8步：Y轴坐标值 + 8
…

2. 找出规律：

1. 每 4 步 一个周期；
2. 用步数除以4取余，余数呈周期；

假设步数为 n ；对 4 取余：\(n\%4\) 。

余1：X轴坐标值 + n
余2：Y轴坐标值 – n
余3：X轴坐标值 – n
余0：Y轴坐标值 + n

3. 测算 2017 步的坐标所在象限：

2017步：\(2017\%4=1\)
说明此时横坐标位于X轴，正向。

上一步，2016步：\(2016\%4=0\)
说明此时纵坐标位于Y轴，正向。

所以2017的坐标应该位于第一象限。

X轴坐标值：

\(
\begin{align*}
&1-3+5-7+9+\cdots+2017 \\
&=1+(-3+5-7+9+\cdots-2015+2017) \\
&=1+[(-3+5)+(-7+9)+\cdots+(-2015+2017)] \\
&=1+\frac{n-1}{4}\times2 \\
&=1+\frac{2017-1}{4}\times2 \\
&=1+\frac{2016}{4}\times2 \\
&=1+504\times2 \\
&=1+1008 \\
&=1009
\end{align*}
\)

Y轴坐标值：

\(
\begin{align*}
&-2+4-6+8-\cdots-2014+2016 \\
&=(-2+4)+(-6+8)-\cdots+(-2014+2016) \\
&=\frac{n}{4}\times2 \\
&=\frac{2016}{4}\times2 \\
&=504\times2 \\
&=1008
\end{align*}
\)

所以最终坐标是（1009，1008）。