【题目】

前缀表达式 *+ab+cd 的中缀表达式形式是（）

A. (a + b) * (c + d)
B. a + b * c + d
C. a * b + c * d
D. (d + c) * (b + a)

【考点】

中缀表达式、前缀表达式、后缀表达式之间的转换。

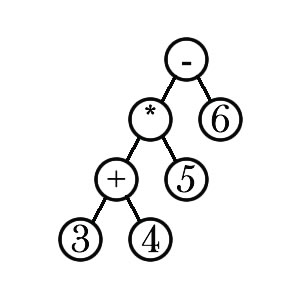
中缀表达式：平常的表达式

\((3+4)\ast5-6=29\)

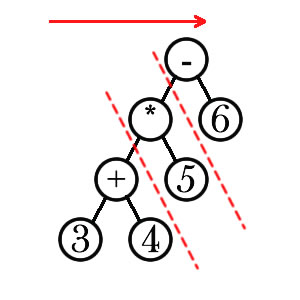
前缀表达式：运算符位于数字前面

\(-\ast+3456=29\)

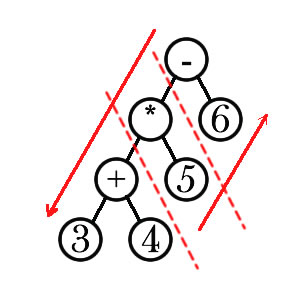
后缀表达式：运算符位于数字后面

\(34+5\ast6-=29\)

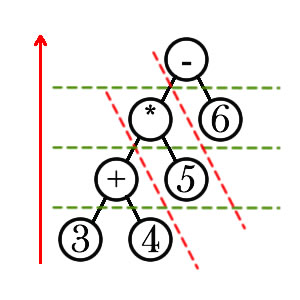
参考：https://www.nowcoder.com/questionTerminal/d9debe1aa2e44b56bea501c0b2a95da3

参考：https://uploadfiles.nowcoder.com/images/20190810/242025553_1565446179857_F843CF887D23FAE6E6081B42358AC012

例如：后缀表达式转中缀表达式

\(ab+cd+\ast\)

后缀表达式转为中缀表达式要点：遇到操作数都进栈，等到碰到运算符就把栈顶两个元素出栈，运算后再入栈，直到结束。

1. a入栈，b入栈，`栈为 a b`
2. 遇到运算符+，b出栈，a出栈，运算为(a+b),再入栈，栈为`(a+b)`
3. c入栈，d入栈，栈为`(a+b) c d`
4. 遇到运算符+,d出栈，c出栈，运算为(c+d),入栈，结果为`(a+b) (c+d)`
5. 遇到运算符*，栈顶两个元素出栈，运算结果为(a+b)*(c+d)

例如：中缀表达式转后缀表达式（从左到右扫描）

\(a\ast{f}+(b-c/d)\ast{e}\)

分为两个栈，结果栈和运算栈，遇到的情况有：
1. 如果是操作数(数字、字母)，则进入结果栈；
2. 如果是左括号，那么入运算栈；
3. 如果是右括号，那么把运算栈的栈顶元素出栈，入栈到结果栈，直到遇到左括号，遇到左括号后，这一对括号都消灭；
4.1 如果是运算符，如果运算栈为空，那么入栈；
4.2 如果是运算符，此时运算栈顶运算符不为左括号，且栈里不存在优先级大于或等于该运算符的运算符，则该运算符入栈，
否则大于等于该运算符的其他运算符先出栈再入栈到结果栈；
4.3 如果是运算符，此时栈顶运算符是左括号，那么入栈。

扫描过程：
1. a 是操作数，进结果栈；结果栈为 a ；
2. * 是运算符，运算栈空，进运算栈；
3. f 是操作数，进结果栈；结果栈为 a f ；
4. + 是运算符，但是栈中存在优先级大于等于的 * ，所以 * 先出栈，然后 * 入运算栈；结果栈为 a f * ；
5. ( 是左括号，入运算栈；运算栈为 + ( ；
6. b 是操作数，入结果栈；结果栈为 a f * b ；
7. – 是运算符，栈顶元素是左括号，所以 – 入运算栈；运算栈为 + ( – ；
8. c 是操作数，入结果栈；结果栈为 a f * b c ；
9. / 是运算符，运算栈顶元素不是左括号，运算栈 + ( – 不存在优先级大于等于 / 的元素，所以 / 入运算栈；
10. d 是操作数，入结果栈；结果栈为 a f * b c d ；
11. ) 是右括号，运算栈的栈顶元素出栈，直到左括号，入栈后进到结果栈；
12. 此时运算栈是 + ( – / ，所以结果栈变为 a f * b c d / – ，运算栈变为 + ，左右括号消灭了；
13. 然后 * 是运算符，运算栈中不存在大于等于的元素，所以入运算栈；运算栈为 + * ；
14. e 是操作数，e 入结果栈；结果栈为 a f * b c d / – e ；
15. 扫描结束，所以运算栈全部出栈到结果栈，为 a f * b c d / – * + 。

【解析】

从右到左扫描整个算式，后扫描到的变量写在前面。

答案是 A