进位计数制:
数的表示规则称为数制。
按照进位方式计数的数制叫进位计数制。
进位计数制由:
1. 一组数码符号;
2. 两个基本因素“基数”与“位权”构成。
基数:进位计数制中所采用的数码(数制中用来表示“量”的符号)的个数。例如:二进制的基数为2。
位权:进位计数制中每一固定位置对应的单位值。
任何一个R进制的数都是由一串数码表示的,其中每一位数码所表示的实际值的大小,除与数字本身的数值有关外,还与它所处的位置有关。该位置上的基准值就称为位权(或位值)。
位权用基数R的i次幂表示。对于R进制数,小数点前第1位的位权为 \(R^1\),小数点前第2位的位权为 \(R^2\),小数点后第1位的位权为 \(R^-1\),小数点后第2位的位权为 \(R^-2\),以此类推。
假设一个R进制数具有n位整数,m位小数,那么其位权为 \(R^i\),其中 i=-m~n-1。显然,对于任一R进制数,其最右边数码的位权最小,最左边数码的位权最大。
任一R进制数的值都可表示为:各位数码本身的值与其所在位位权的乘积之和。
十进制数256.16按位权展开式:\((256.16)10=2*10^2+5*10^1+6*10^0+1*10^-1+6*10^-2\)
二进制数101.01按位权展开式:\((101.01)2=1*2^2+0*2^1+1*2^0+0*2^-1+1*2^-2\)
八进制数307.4按位权展开式:\((307.4)8=3*8^2+0*8^1+7*8^0+4*8^-1\)
十六进制数F2B按位权展开式:\((F2B)16=15*16^2+2*16^1+11*16^0\)
各个进制的表示方法:
| 十进制 | 八进制 | 十六进制 | 二进制 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 01 |
| 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 11 |
| 4 | 4 | 4 | 100 |
| 5 | 5 | 5 | 101 |
| 6 | 6 | 6 | 110 |
| 7 | 7 | 7 | 111 |
| 8 | 10 | 8 | 1000 |
| 9 | 11 | 9 | 1001 |
| 10 | 12 | A | 1010 |
| 11 | 13 | B | 1011 |
| 12 | 14 | C | 1100 |
| 13 | 15 | D | 1101 |
| 14 | 16 | E | 1110 |
| 15 | 17 | F | 1111 |
| 16 | 20 | 10 | 10000 |
| 17 | 21 | 11 | 10001 |
1. 二进制(binary):
0,1 ;满2进1(以0b或0B开头)
如:\(0b101\)
整数常量默认是int类型,当用二进制定义整数时,其第32位是符号位;当是long类型时,二进制默认占64位,第64位是符号位。
数字在计算机底层都是以二进制的形式存储的,且所有的数值,不管正负,底层都以补码的方式存储。
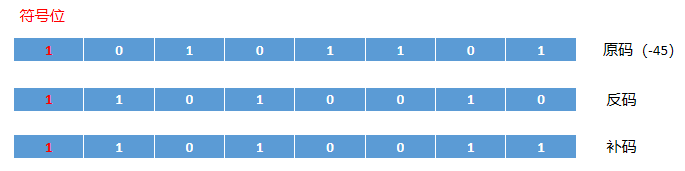
二进制的整数有如下三种形式:
①原码:直接将一个数值换成二进制数,最高位是符号位(正数三码合一)。
②负数的反码:对原码按位取反,只是最高位(符号位)确定为1。
③负数的补码:其反码加1。
2. 八进制(octal):
0-7 满8进1(以数字0开头)
如:\(0101\)
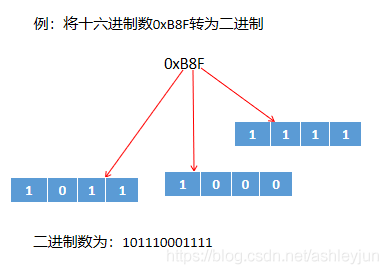
3. 十六进制(hex):
0-9及A-F 满16进1(以0x或0X开头)
如:\(0x11\)
4. 十进制(decimal):
0-9 满10进1(十进制正常输出,不能以0作为开头,除非这个数字本身就是0。)
如:\(1677\)
各个进制数之间的转换:
1. 二进制和十进制之间的转换
①二进制转十进制:

②十进制转二进制:

2. 二进制和八进制之间的转换
①二进制转八进制
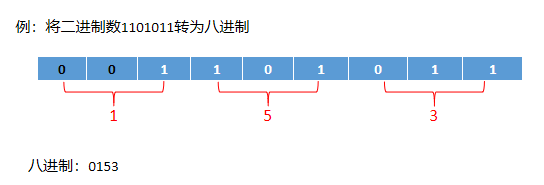
②八进制转二进制
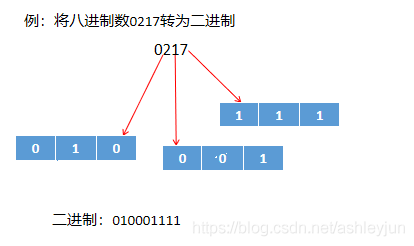
3. 二进制和十六进制之间的转换
①二进制转十六进制
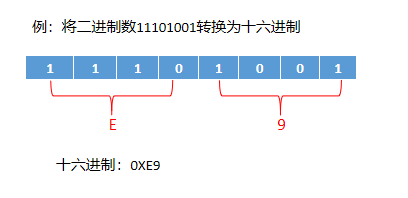
②十六进制转二进制